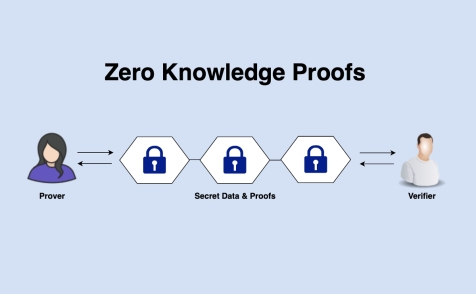
إثبات المعرفة الصفرية

في التشفير ، يعد إثبات عدم المعرفة أو بروتوكول المعرفة الصفرية طريقة يمكن من خلالها لأحد الأطراف (المُثبِت) أن يثبت لطرف آخر (المدقق) أن بيانًا معينًا صحيحًا بينما يتجنب المُثقف نقل أي معلومات إضافية بصرف النظر عن حقيقة أن البيان صحيح بالفعل. إن جوهر براهين عدم المعرفة الصفرية هو أنه من التافه إثبات أن المرء يمتلك معرفة بمعلومات معينة بمجرد الكشف عنها ؛ التحدي هو إثبات هذا الحيازة دون الكشف عن المعلومات نفسها أو أي معلومات إضافية. إذا كان إثبات البيان يتطلب أن يمتلك المُثبِّت بعض المعلومات السرية ، فلن يتمكن المدقق من إثبات البيان لأي شخص آخر دون حيازة المعلومات السرية. يجب أن يشتمل البيان الذي يتم إثباته على التأكيد على أن المُثبِت لديه مثل هذه المعرفة ، ولكن دون تضمين أو نقل المعرفة نفسها في التأكيد. خلاف ذلك ، لن يتم إثبات البيان في المعرفة الصفرية لأنه يزود المدقق بمعلومات إضافية حول البيان بنهاية البروتوكول. إن إثبات المعرفة الصفري هو حالة خاصة عندما يتكون البيان فقط من حقيقة أن المُثبِت يمتلك المعلومات السرية.

تتطلب براهين المعرفة الصفرية التفاعلية تفاعلًا بين الفرد (أو نظام الكمبيوتر) لإثبات معرفتهم والفرد الذي يتحقق من صحة الدليل.
يجب أن يتطلب البروتوكول الذي ينفذ براهين المعرفة الصفرية للمعرفة مدخلات تفاعلية من المدقق. عادة ما تكون هذه المدخلات التفاعلية في شكل تحدٍ واحد أو أكثر بحيث تقنع الردود الواردة من المدقق إذا وفقط إذا كانت العبارة صحيحة ، أي إذا كان المُثبِت يمتلك المعرفة المطالب بها. إذا لم يكن الأمر كذلك ، يمكن للمدقق تسجيل تنفيذ البروتوكول وإعادة تشغيله لإقناع شخص آخر بأنه يمتلك المعلومات السرية. قبول الطرف الجديد له ما يبرره لأن معيد التشغيل يمتلك المعلومات (مما يعني أن معلومات البروتوكول المسربة ، وبالتالي ، لم يتم إثباتها في حالة انعدام المعرفة) ، أو أن القبول زائف ، أي أنه تم قبوله من شخص لا يفعل ذلك. في الواقع تمتلك المعلومات.

توجد بعض أشكال براهين المعرفة الصفرية غير التفاعلية ، لكن صحة الدليل تعتمد على افتراضات حسابية (عادةً افتراضات دالة تجزئة تشفير مثالية).

أمثلة مجردة
كهف علي بابا

تأخذ Peggy بشكل عشوائي إما المسار A أو B ، بينما ينتظر فيكتور في الخارج

يختار فيكتور طريق الخروج

تظهر Peggy بشكل موثوق عند خروج أسماء فيكتور
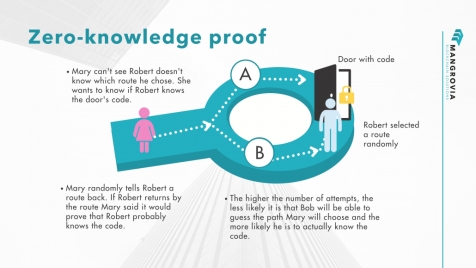
هناك قصة معروفة تقدم الأفكار الأساسية لبراهين انعدام المعرفة ، نُشرت لأول مرة في عام 1990 من قبل جان جاك كيسكواتر وآخرون في ورقتهم “كيف تشرح بروتوكولات المعرفة الصفرية لأطفالك”. [4] من الشائع تسمية الطرفين في إثبات عدم المعرفة على أنهما بيجي (مَثَل البيان) وفيكتور (المتحقق من البيان).

في هذه القصة ، كشفت بيغي النقاب عن الكلمة السرية المستخدمة لفتح باب سحري في كهف. الكهف على شكل حلقة ، المدخل من جانب والباب السحري يسد الجانب الآخر. يريد فيكتور أن يعرف ما إذا كانت بيغي تعرف الكلمة السرية. لكن بيغي ، كونها شخصية خاصة جدًا ، لا تريد أن تكشف عن معرفتها (الكلمة السرية) لفيكتور أو أن تكشف حقيقة معرفتها للعالم بشكل عام.

قاموا بتسمية المسارين الأيسر والأيمن من المدخل A و B. أولاً ، ينتظر فيكتور خارج الكهف بينما تدخل Peggy. تأخذ Peggy إما المسار A أو B ؛ لا يُسمح لفيكتور برؤية المسار الذي تسلكه. بعد ذلك ، يدخل فيكتور الكهف ويصرخ باسم المسار الذي يريد منها أن تستخدمه للعودة ، إما A أو B ، المختار عشوائيًا. شريطة أن تعرف حقًا الكلمة السحرية ، فهذا أمر سهل: تفتح الباب ، إذا لزم الأمر ، وتعود على طول المسار المطلوب.

ومع ذلك ، افترض أنها لا تعرف الكلمة. بعد ذلك ، لن تتمكن من العودة بالمسار المحدد إلا إذا أعطت فيكتور اسم نفس المسار الذي دخلت من خلاله. نظرًا لأن فيكتور سيختار A أو B بشكل عشوائي ، سيكون لديها فرصة 50٪ للتخمين بشكل صحيح. إذا كرروا هذه الحيلة عدة مرات ، لنقل 20 مرة على التوالي ، فإن فرصتها في توقع جميع طلبات فيكتور بنجاح ستصبح صغيرة جدًا (1 من 220 ، أو تقريبًا 1 من كل مليون).

وبالتالي ، إذا ظهر بيغي مرارًا وتكرارًا عند خروج أسماء فيكتور ، فيمكنه أن يستنتج أنه من المحتمل جدًا أن تكون بيجي تعرف الكلمة السرية في الواقع.

ملاحظة جانبية واحدة فيما يتعلق بالمراقبين الخارجيين: حتى لو كان

أو ترتدي كاميرا خفية تسجل المعاملة بأكملها ، فإن الشيء الوحيد الذي ستسجله الكاميرا هو في حالة واحدة صاح فيكتور “A!” و Peggy يظهر في A أو في الحالة الأخرى يصيح فيكتور “B!” وظهور Peggy في B. سيكون تسجيل من هذا النوع تافهًا لأي شخصين لتزييفه (يتطلب فقط أن يتفق Peggy و Victor مسبقًا على تسلسل A و B الذي سيصرخ به فيكتور). بالتأكيد لن يكون مثل هذا التسجيل مقنعًا لأي شخص سوى المشاركين الأصليين. في الواقع ، حتى الشخص الذي كان حاضرًا كمراقب في التجربة الأصلية لن يكون مقتنعًا ، لأن فيكتور وبيغي ربما يكونا قد نسقا “التجربة” بأكملها من البداية إلى النهاية.

لاحظ أيضًا أنه إذا اختار فيكتور علامات A و B الخاصة به عن طريق قلب عملة معدنية على الكاميرا ، فإن هذا البروتوكول يفقد خاصية المعرفة الصفرية ؛ من المحتمل أن يكون قلب العملة على الكاميرا مقنعًا لأي شخص يشاهد التسجيل لاحقًا. وهكذا ، على الرغم من أن هذا لا يكشف عن الكلمة السرية لفيكتور ، إلا أنه يجعل من الممكن لفيكتور إقناع العالم بشكل عام بأن بيجي لديها تلك المعرفة – وهذا يتعارض مع رغبات بيجي المعلنة. ومع ذلك ، فإن التشفير الرقمي عمومًا “يقلب العملات المعدنية” من خلال الاعتماد على مولد أرقام شبه عشوائي ، والذي يشبه عملة معدنية ذات نمط ثابت من الرؤوس وذيول لا يعرفها إلا مالك العملة. إذا تصرفت عملة فيكتور بهذه الطريقة ، فسيكون من الممكن مرة أخرى أن يقوم فيكتور وبيغي بتزييف “التجربة” ، لذا فإن استخدام مولد الأرقام العشوائية الزائفة لن يكشف عن معرفة بيجي للعالم بنفس الطريقة التي يستخدم بها استخدام عملة معدنية مقلوبة كان.

لاحظ أن Peggy يمكن أن تثبت لفيكتور أنها تعرف الكلمة السحرية ، دون أن تكشفها له ، في تجربة واحدة. إذا ذهب كل من فيكتور وبيجي معًا إلى مدخل الكهف ، فيمكن لفيكتور مشاهدة Peggy وهي تدخل من خلال A وتخرج من خلال B. وهذا سيثبت على وجه اليقين أن Peggy تعرف الكلمة السحرية ، دون الكشف عن الكلمة السحرية لفيكتور. ومع ذلك ، يمكن ملاحظة مثل هذا الدليل من قبل طرف ثالث ، أو تسجيله بواسطة فيكتور ، وسيكون مثل هذا الدليل مقنعًا لأي شخص. بعبارة أخرى ، لم تستطع بيغي دحض مثل هذا الدليل بالادعاء بأنها تواطأت مع فيكتور ، وبالتالي فهي لم تعد تتحكم في من يدرك معرفتها.

كرتان والصديق المصاب بعمى الألوان
تخيل أن صديقك “فيكتور” مصاب بعمى الألوان الأحمر والأخضر (بينما أنت لست كذلك) ولديك كرتان: واحدة حمراء والأخرى خضراء ، لكنهما متطابقتان. بالنسبة لفيكتور ، تبدو الكرات متطابقة تمامًا. يشك فيكتور في أن الكرات يمكن تمييزها بالفعل. تريد أن تثبت لفيكتور أن الكرات في الواقع ذات ألوان مختلفة ، لكن لا شيء آخر. على وجه الخصوص ، لا تريد الكشف عن الكرة الحمراء وأيها الخضراء.

هنا نظام الإثبات. أنت تعطي الكرتين لفيكتور ويضعهما خلف ظهره. بعد ذلك ، يأخذ إحدى الكرات ويخرجها من خلف ظهره ويعرضها. ثم وضعه خلف ظهره مرة أخرى ثم اختار الكشف عن واحدة فقط من الكرتين ، واختيار واحدة من الاثنين عشوائياً باحتمالية متساوية. سوف يسألك ، “هل قمت بتبديل الكرة؟” ثم يتم تكرار هذا الإجراء برمته كلما لزم الأمر.

من خلال النظر إلى ألوان الكرات ، يمكنك ، بالطبع ، أن تقول على وجه اليقين ما إذا كان قد قام بتبديلها أم لا. من ناحية أخرى ، إذا كانت الكرات بنفس اللون وبالتالي لا يمكن تمييزها ، فلا توجد طريقة يمكنك تخمينها بشكل صحيح مع احتمال أعلى من 50٪.

نظرًا لأن احتمال نجاحك بشكل عشوائي في تحديد كل مفتاح / غير مفتاح هو 50٪ ، فإن احتمال نجاحك عشوائيًا في جميع المفاتيح / عدم التبديل يقترب من الصفر (“السلامة”). إذا كررت أنت وصديقك هذا “الإثبات” عدة مرات (على سبيل المثال 20 مرة) ، يجب أن يقتنع صديقك (“الاكتمال”) بأن الكرات ملونة بشكل مختلف بالفعل.

الدليل أعلاه هو عدم المعرفة لأن صديقك لا يعرف أبدًا أي كرة خضراء وأيها حمراء ؛ في الواقع ، لم يكتسب أي معرفة حول كيفية التمييز بين الكرات.

تعريف

يجب أن يستوفي دليل المعرفة الصفرية لبعض العبارات ثلاث خصائص:

الاكتمال: إذا كان البيان صحيحًا ، فإن المحقق الصادق (أي الذي يتبع البروتوكول بشكل صحيح) سيقتنع بهذه الحقيقة بمثل صادق.
الصحة: إذا كانت العبارة خاطئة ، فلا يمكن لمثل غش أن يقنع المحقق الصادق بصحتها ، إلا مع وجود احتمال ضئيل.
المعرفة الصفرية: إذا كانت العبارة صحيحة ، فلن يتعلم أي محقق أي شيء بخلاف حقيقة أن العبارة صحيحة. بعبارة أخرى ، يكفي مجرد معرفة العبارة (وليس السر) لتخيل سيناريو يُظهر أن المُثبِّت يعرف السر. يتم إضفاء الطابع الرسمي على ذلك من خلال إظهار أن كل محققلديه بعض المحاكاة التي ، بالنظر إلى العبارة المراد إثباتها فقط (وعدم إمكانية الوصول إلى المُثبِّت) ، يمكن أن تنتج نصًا “يشبه” التفاعل بين المُثبِّت الصادق والمحقق المعني.